目录
1.来源:
2.哈希函数
1.哈希函数的设计规则
2.哈希函数的设计思路
3.哈希碰撞
4.解决哈希碰撞的方案
5.负载因子
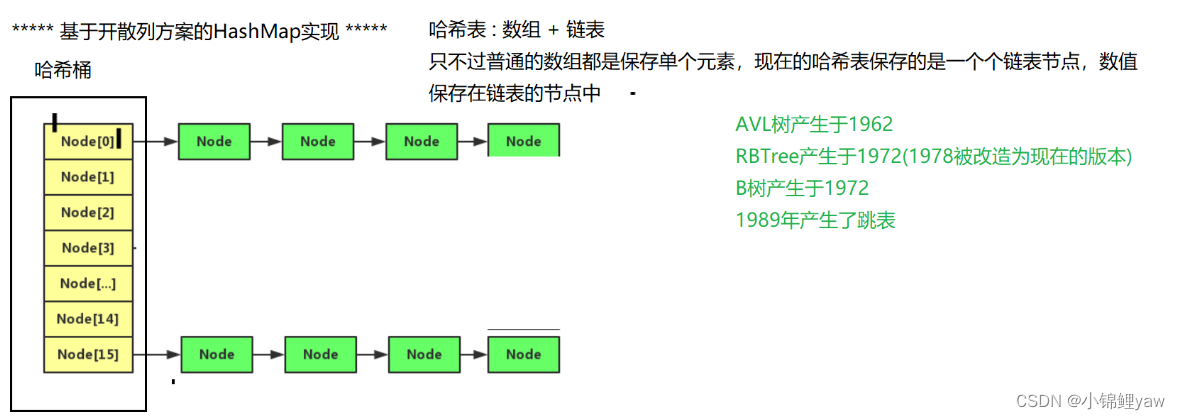
3.基于开散列方案的HashMap实现
1.HashMap类中的属性
2.哈希函数
3.判断当前哈希表中是否含有指定的key值
4.判断当前哈希表中是否包含指定的value值
5.在哈希表中新增,修改元素
6.哈希表扩容
7.删除哈希表中指定的key节点
1.来源:
哈希表来源于数组的随机访问特性
当我们需要查找某个指定元素时,
用平衡搜索树存储:时间复杂度为O(logn)
用数组存储,如果知道了元素的索引,那么查找元素的时间复杂度就是O(1)
利用数组的随机访问特性来查找元素,这个思想就是哈希表产生的背景
2.哈希函数
1.哈希函数的设计规则

2.哈希函数的设计思路

3.哈希碰撞
哈希碰撞是指两个不同的值经过哈希函数计算之后得到相同的值,不论是多优秀的哈希函数,哈希碰撞都不可避免,我们只能尽量降低哈希碰撞出现的概率
取一个素数作为负载因子可以有效降低哈希碰撞的几率
4.解决哈希碰撞的方案
1.闭散列(线性探测):发生冲突时,找冲突旁边的空闲位置放入冲突元素
虽然好想好放,但是因此带来的更大问题,难找更难删,所以一般不采用
2.开散列(链地址法):出现冲突,让冲突的位置变成一个链表
就这样做解决了一部分问题,但随着数据的不断增加,哈希冲突的概率不断增大,在当前数组中,某些链表的长度会很长,查找效率依然下降
解决方案:
1.整个数组扩容,对数组内元素进行搬移,原先冲突的元素大概率不会在冲突
2.将长度过于长的链表转为BST
5.负载因子

3.基于开散列方案的HashMap实现
1.HashMap类中的属性
private static class Node{
int key;
int value;
Node next;
public Node(int key, int value) {
this.key = key;
this.value = value;
}
}
private int size;
private int M;
private Node[] data;
//负载因子
private static final double LOAD_FACTOR = 0.75;
public MyHashMap(int capacity) {
this.data = new Node[capacity];
this.M = capacity;
}
public MyHashMap() {
this(16);
}2.哈希函数
//哈希函数
private int hash(int key) {
return key % this.M;
}3.判断当前哈希表中是否含有指定的key值
//判断当前哈希表中是否含有指定的key值
public boolean containsKey(int key){
int index = hash(key);
for (Node i = data[index]; i != null ; i = i.next) {
if(i.key == key) {
return true;
}
}
return false;
}
4.判断当前哈希表中是否包含指定的value值
//判断当前哈希表中是否包含指定的value值
public boolean containsValue(int value) {
for(int i = 0; i < data.length; i++) {
for(Node x = data[i]; x != null; x = x.next) {
if(x.value == value) {
return true;
}
}
}
return false;
}5.在哈希表中新增,修改元素
//在哈希表中新增,修改元素
public int put(int key, int value) {
int index = hash(key);
//判断是否存在
for(Node x = data[index]; x != null; x = x.next) {
if(x.key == key) {
int oldValue = x.value;
x.value = value;
return oldValue;
}
}
//此时一定不存在
Node node = new Node(key,value);
node.next = data[index];
data[index] = node;
size++;
//判断是否需要扩容
if(size >= data.length * LOAD_FACTOR) {
resize();
}
return -1;
}6.哈希表扩容
private void resize() {
this.M = data.length << 1;
Node [] newData = new Node[M];
for (int i = 0; i < data.length; i++) {
for (Node x = data[i]; x != null;) {
Node next = x.next;
int newIndex = hash(x.key);
x.next = newData[newIndex];
newData[newIndex] = x;
x = next;
}
}
data = newData;
}
7.删除哈希表中指定的key节点
//删除哈希表中指定的key节点
public boolean removeKey(int key) {
int index = hash(key);
//判空
if(data[index] == null) {
return false;
}
//判断是否为头节点
if(data[index].key == key) {
data[index] = data[index].next;
size--;
return true;
}
Node prev = data[index];
while (prev.next != null) {
if(prev.next.key == key) {
prev.next = prev.next.next;
size--;
return true;
}
}
return false;
}


![Redis使用教程之jedis客户端sendCommand方法的byte[]入参,防止混淆string的byte与数值byte的区别](/images/no-images.jpg)

